The Virtual cellular automaton

This is an automaton invented by Gary Shannon (see the original page; some gates are taken from this page). It is a 2D, totalistic automaton with Moore neighboorhood and 4 different states: black, grey, empty and border. The grey state is a virtual cell, because it is not counted as a neighbor. The rules:

1. A black cell turns into a grey cell on the next generation, regardless of its neighbors.
2. A grey cell turns into an empty cell on the next generation, regardless of its neighbors.
3. An empty cell turns into a black cell, if the number of black neighbors are 1 or 3.

A "battery", which emits one black cell every 4 ticks:

A battery, which emits one black cell every 3 ticks:

The XOR gate, built with a T-joint:

With a battery and an XOR gate, a NOT gate is possible:

At the bottom you can see a curve, which is not part of the XOR gate.

To cross two signal paths, a crossover device is needed (the idea was posted to the comp.theory.cell-automata newsgroup by Paul Chapman for this CA, but John von Neumann has invented a similiar gate for his Universal Constructor many years ago). The crossover is built with curves, XOR gates and an inverse T-joint, which splits an incoming signal into two signals. The crossover works with a space of one cells, too, as the following animation shows:

You can't emulate all logic operations with XOR and NOT, only. Another gate is needed. I've found a NOT IMPLICATION gate. The implication A => B is false only, if A is true and B is false:

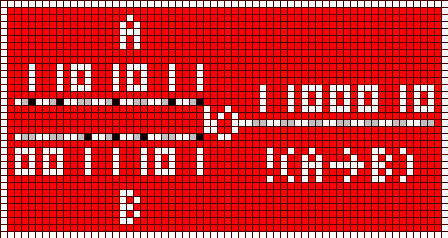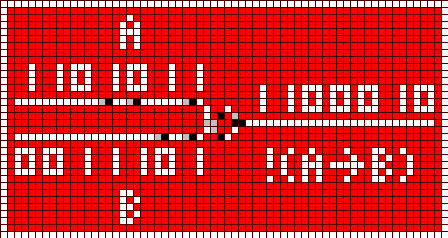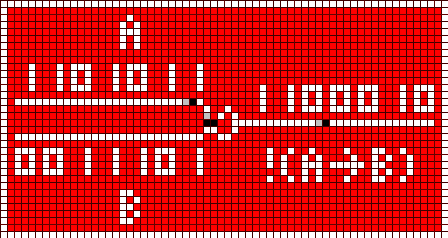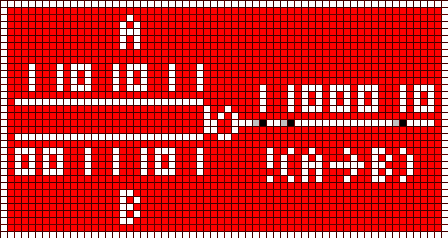
It's easy to built a NOR with a NOT IMPLICATION and a NOT gate (written as "!"), as the following logic table shows:

With this gates all other gates can be built to construct a computer.

Another symbolic approach: Paul Chapman calculated a "AND NOT" operation:

!(A => B) = !(!A AND B) = A AND !B

and with this, and the NOT operator, the AND and OR operators are possible:

A AND B = A AND !(!B)

A OR B = !(!A AND !B)     [DeMorgan's Law]

Because XOR is easier to built than NOT, it is useful to built AND and OR with AND! and XOR alone:

NAND is an AND with a NOT at the output, so all gates exists to construct a computer (NAND alone would be sufficient).

All gate files zipped in MCell format. To make it look like the animations on this page, with black/grey/white/red cells, copy the file "virtual.mcp" from the gate zip file to the MCell\System directory. After restarting MCell you can select it from the menu Colors->PaletteSelection->Virtual.